La largeur de la fente étant
de l'ordre de quelques dizaines de microns, les méthodes simples
accessibles à des amateurs sont :
la diffraction par un laser,
l'observation sous microscope,
la projection avec un projecteur-diapos.
La diffraction par laser est un TP classique des classes terminales de lycée, qui consiste à envoyer le faisceau de lumière d'un laser dans une fente étroite : on observe alors sur un écran placé derrière la fente une série de taches lumineuses séparées par des taches sombres.
Rappelons que la diffraction est un phénomène caractéristique des ondes, qui se produit à chaque fois qu'une onde rencontre un obstacle. Cet obstacle devient lui-même émetteur d'ondelettes sphériques par toute sa surface de contact avec l'onde. Ces ondelettes se composent entre elles, produisant des interférences qui se traduisent par des zônes d'obscurité et des zônes de pleine lumière réparties régulièrement dans l'espace selon des lois simples bien établies.
Voir le "Guide Utilisateur" du Lhires, page 15 :
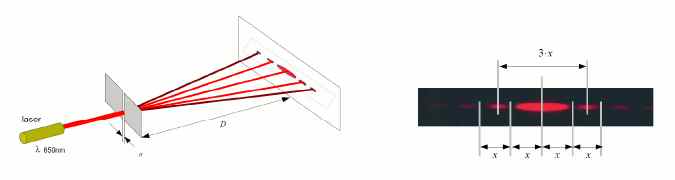
Soit "a" la largeur de la fente, D la distance fente-écran sur lequel on mesure l'espace "x" entre deux taches sombres, et λ la longueur d'onde de la lumière émise par le laser. La relation entre les grandeurs impliquées dans l'expérience est : a = λ.D/x
Valeurs de "x" (en mm) obtenues théoriquement pour diverses valeurs de largeur de fente "a" en µm, et de la distance "D" en mètres :
Pour nous, le but de la manip est d'obtenir la valeur de "a" à partir des mesures de "x", de D, et de λ.
Par exemple pour D = 2 m, avec un laser rouge de λ = 650 nm, si on mesure 3x = 21 cm, on en déduit la valeur de a = 0,650×2000/70 = 18,6 µm.
La question qui se pose est de connaitre la précision de cette mesure. On peut faire un calcul d'incertitudes à partir de la formule a = λ.D/x.
La formule des incertitudes relatives donne :
Δa/a = Δλ/λ + ΔD/D + Δx/x
en appelant Δa l'incertitude absolue sur a, etc...
estimons les incertitudes sur les grandeurs mesurées : pour λ on peut utiliser le Lhires pour la mesurer, pour D on peut estimer l'incertitude sur la valeur de 2 m à 0,5 cm :ΔD/D = 0,5/200
en ce qui concerne "x", on obtient sa valeur à partir de la mesure d'une longueur L, que l'on divise ensuite par un nombre d'intervalles n : x = L/n
Δx/x = ΔL/L
la mesure de L n'est pas très précise car on a du mal à situer exactement la position des zônes obscures sur l'écran à mieux que 0,5 cm et parfois 1cm.
prenons ΔL/L = 0,5/21
Mesurons ensuite la longueur d'onde du laser avec le Lhires, en haute résolution 2400 t/mm, et avec le néon comme référence.

La longueur d'onde principale vaut 654,4 nm mettons à 0,1 nm près.
Dans ce cas, "a" vaut : 0,6544×2000/70 = 18,7 µm
L'incertitude sur "a" peut maintenant se calculer :
Δa/a = 0,1/654,4 + 0,5/200 + 0,5/21 = 0,0264 = 2,6 % d'où on tire Δa = a×0,0264 = 0,494 µm < 0,5 µm
On peut encadrer la valeur probalble de "a" : 18,2 µm < a < 19,2 µm
Avec ne mesure de L faite à 1 cm près, l'incertitude sur "a" aurait doublé : 5 %, d'où une incertitude absolue de 1 µm sur la valeur de "a" et un encadrement :
17,7 µm < a < 19,7 µm
la diffraction par un laser,
l'observation sous microscope,
la projection avec un projecteur-diapos.
La diffraction par laser est un TP classique des classes terminales de lycée, qui consiste à envoyer le faisceau de lumière d'un laser dans une fente étroite : on observe alors sur un écran placé derrière la fente une série de taches lumineuses séparées par des taches sombres.
Rappelons que la diffraction est un phénomène caractéristique des ondes, qui se produit à chaque fois qu'une onde rencontre un obstacle. Cet obstacle devient lui-même émetteur d'ondelettes sphériques par toute sa surface de contact avec l'onde. Ces ondelettes se composent entre elles, produisant des interférences qui se traduisent par des zônes d'obscurité et des zônes de pleine lumière réparties régulièrement dans l'espace selon des lois simples bien établies.
Voir le "Guide Utilisateur" du Lhires, page 15 :

Soit "a" la largeur de la fente, D la distance fente-écran sur lequel on mesure l'espace "x" entre deux taches sombres, et λ la longueur d'onde de la lumière émise par le laser. La relation entre les grandeurs impliquées dans l'expérience est : a = λ.D/x
Valeurs de "x" (en mm) obtenues théoriquement pour diverses valeurs de largeur de fente "a" en µm, et de la distance "D" en mètres :
| λ : 650 nm | 650 | D | ||
| 0.5 | 1 | 2 | ||
| a | 10 | 32.5 | 65 | 130 |
| 20 | 16.25 | 32.5 | 65 | |
| 30 | 10.8 | 21.7 | 43.3 | |
Pour nous, le but de la manip est d'obtenir la valeur de "a" à partir des mesures de "x", de D, et de λ.
Par exemple pour D = 2 m, avec un laser rouge de λ = 650 nm, si on mesure 3x = 21 cm, on en déduit la valeur de a = 0,650×2000/70 = 18,6 µm.
La question qui se pose est de connaitre la précision de cette mesure. On peut faire un calcul d'incertitudes à partir de la formule a = λ.D/x.
La formule des incertitudes relatives donne :
Δa/a = Δλ/λ + ΔD/D + Δx/x
en appelant Δa l'incertitude absolue sur a, etc...
estimons les incertitudes sur les grandeurs mesurées : pour λ on peut utiliser le Lhires pour la mesurer, pour D on peut estimer l'incertitude sur la valeur de 2 m à 0,5 cm :ΔD/D = 0,5/200
en ce qui concerne "x", on obtient sa valeur à partir de la mesure d'une longueur L, que l'on divise ensuite par un nombre d'intervalles n : x = L/n
Δx/x = ΔL/L
la mesure de L n'est pas très précise car on a du mal à situer exactement la position des zônes obscures sur l'écran à mieux que 0,5 cm et parfois 1cm.
prenons ΔL/L = 0,5/21
Mesurons ensuite la longueur d'onde du laser avec le Lhires, en haute résolution 2400 t/mm, et avec le néon comme référence.

La longueur d'onde principale vaut 654,4 nm mettons à 0,1 nm près.
Dans ce cas, "a" vaut : 0,6544×2000/70 = 18,7 µm
L'incertitude sur "a" peut maintenant se calculer :
Δa/a = 0,1/654,4 + 0,5/200 + 0,5/21 = 0,0264 = 2,6 % d'où on tire Δa = a×0,0264 = 0,494 µm < 0,5 µm
On peut encadrer la valeur probalble de "a" : 18,2 µm < a < 19,2 µm
Avec ne mesure de L faite à 1 cm près, l'incertitude sur "a" aurait doublé : 5 %, d'où une incertitude absolue de 1 µm sur la valeur de "a" et un encadrement :
17,7 µm < a < 19,7 µm