CALCUL DE LA DISTANCE DE L'ASTEROIDE EROS

CALCUL DE LA DISTANCE DE L'ASTEROIDE EROS

à partir de l'image donnée sur astrosurf par bbdb.

http://www.astrosurf.com/ubb/Forum3/HTML/034381.html

mesure de la parallaxe par repérage du champ dans CarteduCiel.

les 2 images ont été prises le 3 février 2012 à 3h10 TU

l'une depuis l'observatoire de Calern, l'autre depuis LaSilla (Chili)

avec des télescopes newton semblables et caméras CCD semblables.

la parallaxe mesurée est p = 76"

Calcul de la base de triangulation Calern-Lasilla.

coordonnées géographiques :

Calern (longitude La = 6°55'26" E, lata = 43°45'8" N, altitude ha = 1,27 km) point A

Lasilla (longitude Lb = 70°44' W, latb = 29°15' S, altitude hb = 2,42 km) point B

La longueur du segment droit AB est :

AB = racinecarrée[(xb-xa)²+(yb-ya)²+(zb-za)²]

Les coordonnées rectangulaires des points A et B :

posons Ra = R + ha Rb = R + hb (R = rayon Terre)

Xa = Ra*cos(lata)*cos(La)

Ya = Ra*cos(lata)*sin(La)

Za = Ra*sin(lata)

Xb = Rb*cos(latb)*cos(Lb)

Yb = Rb*cos(latb)*sin(Lb)

Zb = Rb*sin(latb)

Programme Qbasic pour faire ce calcul

CLS

pi = 3.14159

R = 6378

p = 76 'parallaxe en arcsec

REM declaration des variables

ha = 1.27 : hb = 2.42

Ra = R + ha : Rb = R + hb

Latadeg = 43 : latamin = 45 : latasec = 8 'latitude du point A

Latbdeg = -29 : latbmin = -15 'latitude du point B

Ladeg = 6 : Lamin = 55 : Lasec = 26 'longitude du point A

Lbdeg = -70 : Lbmin = -44 'longitude du point B

REM conversion des angles en radians

op = (180*3600)/pi

Lata = (latadeg*3600 + latamin*60 + latasec)/op

Latb = (latbdeg*3600 + latbmin*60)/op

La = (Ladeg*3600 + Lamin*60 + Lasec)/op

Lb = (Lbdeg*3600 + Lbmin*60)/op

REM calcul des coordonnees

Xa = Ra*cos(lata)*cos(La)

Ya = Ra*cos(lata)*sin(La)

Za = Ra*sin(lata)

Xb = Rb*cos(latb)*cos(Lb)

Yb = Rb*cos(latb)*sin(Lb)

Zb = Rb*sin(latb

REM calcul de la distance AB

AB = SQR[(xb-xa)²+(yb-ya)²+(zb-za)²]

PRINT " La longueur de la base est AB = " ; AB

END

..................................................................................................................................................

Résultat : AB = 9896.7 km

..................................................................................................................................................

Avec l'approximation que le triangle AB-Eros est isocele et que la droite centre Terre-Eros est perpendiculaire à la base AB

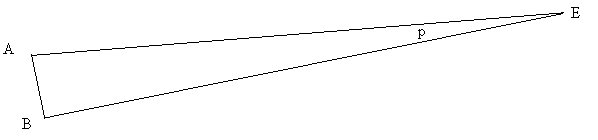
p (radians) = AB/d

D'où d = AB / p = 9896.7 / (76*pi/648000) = 2.686.10^7 km = 0.1796 UA

.........................................................................................................................................................

Lignes Qbasic à ajouter aux précédentes

REM calcul de la distance de l'astéroïde

d = AB*op/p

dua = d / 149500 000

PRINT " La distance de l'asteroide est", d, "km"

PRINT " c'est-à-dire en unités astronomiques",dua, "UA"

END

.........................................................................................................................................................

Le triangle ABE n'est pas forcement parfaitement isocele. Calculons l'angle (AB,AE) en utilisant le produit scalaire AB.AE. La distance AE n'étant pas connue, on peut utiliser un vecteur de module R porté par AE.

Soit v = AE' ce vecteur

Comme on a affaire à des points positionnés avec des systèmes de coordonnées différents, il vaut mieux utiliser le même systeme si l'on veut obtenir des résultats exacts.

Choisissons d'utiliser les coordonnées géographiques terrestres.

On doit alors convertir les coordonnées de l'astéroïde (AD et Déclinaison) en coordonnées terrestres.

La latitude du point E' est la déclinaison de l'astre E.

Pour la longitude, considérons le schéma suivant :

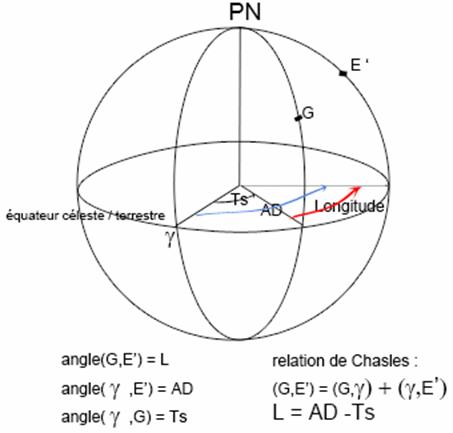
Ts = "temps sidéral de Greenwich" = c'est l'angle séparant le méridien de Greenwich et celui du point vernal.

vx = Rcos(declinaison)*cos(AD-Ts)

vy = Rcos(declinaison)*sin(AD-Ts)

vz = Rsin(declinaison)

les coordonnees du vecteur AB sont

xb-xa

yb-ya

zb-za

AB.v = (xb-xa)*vx + (yb-ya)*vy + (zb-za)*vz = ||AB||*R*cos(AB,v)

(AB,v) = ß

La base de la triangulation vaut :

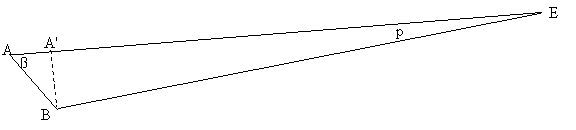A'B ou AB' = AB*sinß

Programme de calcul de l'angle ß en Qbasic, à écrire à la suite du précédent

Deltadeg = -8 'déclinaison asteroide

Deltamin = -6

Deltasec = -5.83

Alphah = 10 'ascension doite asteroide

Alphamin = 29

Alphasec = 45.7

Thetah = 12 'temps sideral de Greenwich

Thetamin = 0

Thetasec = 52

REM conversion des angles en radians

Delta = (deltadeg*3600 + deltamin*60 + deltasec)/op

Alpha = 15*(alphah*3600 + alphamin*60 + alphasec)/op

Theta = 15*(thetah*3600 + thetamin*60 + thetasec)/op

REM calcul des coordonnées du vecteur v

vx = R*cos(delta)*cos(-theta+alpha)

vy = R*cos(delta)*sin(-theta+alpha)

vz = R*sin(delta)

REM calcul du produit scalaire AB.v = ps

ps = (xb-xa)*vx + (yb-ya)*vy + (zb-za)*vz

REM calcul de l'angle beta = (AB,v)

q = ps/AB 'q est le cosinus de beta

PRINT " le cosinus de l'angle beta vaut ", q

REM calcul de la base de triangulation

tri1 = AB*SQR(1-q^2)

PRINT " La base de la triangulation est ", tri1, "km"

PRINT " La distance de l'asteroide est ", tri1*op/p, " km"

END

..........................................................................................................................

Résultats : cosß = 0.079749 (donc ß est très proche de 90°)

Base de triangulation = 9865 km

Distance de l'astéroïde = 26.77 . 10^6 km

= 0.17909 UA

Ce résultat est parfaitement compatible avec ce que donne CarteduCiel : 0.1791 UA

...........................................................................................................................

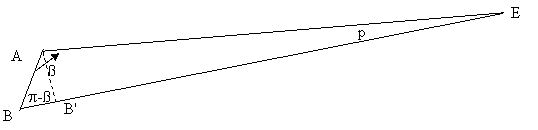
Calcul de l'angle ß en utilisant le produit vectoriel AB^v

Rappel : les vecteur AB et v ont pour coordonnées

xb-xa | vx

yb-ya | vy

zb-za | vz

avec pour le vecteur v :

vx = Rcos(declinaison)*cos(-Ts+AD)

vy = Rcos(declinaison)*sin(-Ts+AD)

vz = Rsin(declinaison)

le produit vectoriel a pour coordonnées :

pvx = (yb-ya)vz-(zb-za)vy

pvy = (zb-za)vx-(xb-xa)vz

pvz = (xb-xa)vy-(yb-ya)vx

module du produit vectoriel :

pv = racine(pvx²+pvy²+pvz²) = ||AB||.v.sinß

sinß = pv / AB

programme Qbasic à ajouter

REM calcul de l'angle beta par produit vectoriel AB^v

pvx = (yb-ya)*vz-(zb-za)*vy

pvy = (zb-za)*vx-(xb-xa)*vz

pvz = (xb-xa)*vy-(yb-ya)*vx

pv = SQR(pvx^2 + pvy^2 + pvz^2)

s = pv / AB 'sinus(beta)

REM nouvelle base de la triangulation

tri2 = AB*s

PRINT " La base de la triangulation est ", tri2, "km"

PRINT " La distance de l'asteroide est ", tri2*op/p, " km"

dista = (tri2*op / p) / 149500000

dista2 = FIX(dist * 100000)

dista3 = dist2 / 100000

PRINT " c'est-a-dire en unites astronomiques"; dista3; "UA"

END

...................................................................................................

Les résultats sont les mêmes qu'avec le produit scalaire.

RETOUR ACCUEIL